I've been trying to figure out how come the only relationship between types we use to encounter is "sub". Type a is a subtype of type b. Validated by subsitution principle.
If we limit ourselves with "sub", we'll have infinite arguments on whether a square can be considered as a subtype of rectangle; whether a colored-point can be considered a subtype of point; whether an int can be considered, under certain conditions, as a subtype of float; whether, in Java, if A implements B, A is a subtype of B. Opinions differ.
I think we should look deeper and maybe consider this case by case.
- Is square a rectangle? Seems so; the objection being that when we start stretching the rectangle, not every square remains a rectangle. Modification is a weird thing. Even in simple cases, i = 1, then (i == 1) becomes true; but it is not actually true, because next moment i = 2, and the expression is false. No temporal logic transforms true into false, there's something wrong there. But if we discard modification, we can state this: each square 'is a' rectangle. We have an injection. Two different squares treated as rectangles remain different.
- Is colored-point a point? This is a totally different case. The world of colored-points is different from the world of points: it is bigger. Yes, a colored-point can be used instead of a point in a substitution. So, in a sense, it 'is a' point. But two different colored-points can become the same point if we forget about their color. Each point 'is a' projection of a colored-point, and eachcolored-point can be treated as a point. So what we have here is a projection here.
- Let's try to implement an unordered-pair. We can do it by taking a pair type and then defining equality in such a way that (a, b) == (b, a). Again, we have a projection, but in this case we went the other way around: not building a new type by adding a dimension, but discovered a new type by defining an equivalence relationship between pairs. So what we have here is a factorization.
- In the case of int -> float, we have a more general case. Not all operations are preserved; not all floats come from ints, and not all two different ints map to two different floats. Still, it is a legal type transformation, done usually by default, called coercion.
- In Java-like languages, if a class implements an interface, it thus declares that it can be used in any context where the interface is required. It projects itself into the realm of the given interface, and that's all we know; the "true nature" of the class implementing an interface remains obscure.
- In the context of 5., the Java keyword "extends" is meaningless. That is, in reality it has many meanings: "borrows the functionality", "implements the same set of interfaces", "has access to internal namespace". Non of this has anything to do with types relationships.
- 'is a' actually has many meanings too. We probably never can be sure whether A 'is a' B: we should always ask: "in which contexts" (that is, "what do you mean?"). If we look at this:
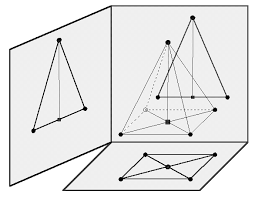 the pyramid here is neither a square nor a triangle. But when projected, it can be percieved as one. If we say "he's a soldier", it does not mean that's all the person is; what we mean is just a projection.
the pyramid here is neither a square nor a triangle. But when projected, it can be percieved as one. If we say "he's a soldier", it does not mean that's all the person is; what we mean is just a projection.So, how about substitution? We can substitute A with B if we know the mapping that maps B into the context where A should be present. If we are talking about coercion (and we know that an int is not a subtype of float), for instance, we can substitute a float with an int value if coercion is legal. In this and other cases, our ability to substitute means we know a canonical mapping.
Now examples.
- Injection. Take types A and B; build A+B, a union. Some languages support unions, some don't. Some support them implicitly, like Scala with its case classes. By definition, there are canonical inclusions from A and B into A+B; so it would be logical to call A and B subtypes of A+B.
- Projection. Take types A and B, and their product, A×B. One can represent A×B as the type of pairs (a, b), with a of type A and b of type B. There are two projections from A×B to A and B. Neither A nor B can be seriously called a subtype of A×B, of course. They can be considered as a special case of factor-types. Below is another example of factor-type.
- Surjection. Given A×A, a type of pairs (a1, a2), we can build a type of unordered pairs by equalizing (a1, a2) with (a2, a1). This gives us an equivalence relationship, and a projection from A×A to A×A /2, the type of unordered pairs.
- Enum surjection. Suppose we build an enum class for Rainbow. It turns out in different cultures the number of colors is different. In China, Japan, Russia, there are seven colors, while in some other countries (US for instance) there are 6. Two colors, light-blue and dark-blue, in Asian rainbow, both map to just blue in US rainbow. So every time we pass a US rainbow instance to a function, we can as well coerce an Asian rainbow ("substitute") into US version, using the standard mapping. It is similar to projection, where the receiving side has no clue about the hidden multiplicity of possible parameter values.
In computer science there is a variety of terms that are supposed to denote this variety of "-typing", but somehow they either are all called kinds of subtyping or declared not to belong to the "-typing" realm. I suggest to apply pretty simple categorical notions, so that things just look simpler and more manageable.
2 comments:
What about ad-hoc derivation and prototype-based derivation?
That's probably a different side of the story. I focused on semantics. Semantically, it does not matter whether we linked our object to superobject manually or using a compiler.
Post a Comment