Here I had introduced countable sets, and
here I had demonstrated how we can build a union of two countable sets. Now is time for Cartesian products.
Suppose we have two sets,
{'A', 'B'} and
{1, 2, 3}. Their product will look like this:
{('A',1), ('A',2), ('A',3), ('B',1), ('B',2), ('B',3)}. It is pretty easy to build: iterate over the first set, and for each element iterate over the second set. In Scala it is pretty easy:
for (a <- setA;
b <- setB) yield (a, b)
The problem is that if the second component (
setB) is infinite, we will never be able to iterate over
all elements. Let
setB be, for instance, the set of all natural numbers,
N. In this case the product
setA x setB will be yielding
('A',0), ('A',1), ('A',2),..., and will never switch to pairs like
('B',i). We have to do something about it.
Say, in the case when only one component is infinite, we could think about changing the order of the loop, first iterating over the infinite component.
That won't work actually. We cannot always know for sure if a set is finite or not.
Halting problem, you know. So we have to figure out how to do it in a general way, without losing common-sense efficiency for the finite case.
The solution has been known for over 100 years, and is called
Kantor Pairing Function.
In this picture:
you see this function enumerating pairs of natural numbers in the following order:
(0,0), (1,0), (0,1), (2,0), (1,1), (0,2), (3,0)... - you got it.
In our case we have two essential differences: first, the sets we have are not necessarily finite, and second, elements are not retrievable by their "sequential numbers"... meaning, it's possible, but it is horribly ineffecient: to reach element #1000, we need to rescan all the elements from #1 (or rather #0, since natural numbers and array indexes start with 0). So we also do not need a fancy formula for Kantor Pairing Function (see link above), the formula that calculates product elements by their sequential numbers. All we need is a way to iterate over elements in the right order.
Okay, let's first write the factory method for Cartesian products:
def product[X, Y](xs: Set[X], ys: Set[Y]): Set[(X, Y)] = {
val predicate = (p: (X, Y)) => xs.contains(p._1) && ys.(p._2)
setOf(
kantorIterator(xs, ys),
xs.size * ys.size,
predicate
)
}
The predicate definition is extracted just for readability purposes. What's important here is
kantorIterator that is supposed to work with any combination of finite and infinite countable sets.
Since we do not have direct access to the elements of the sets by their indexes, we will, instead, keep the rows in iterators. Note that we can build a queue of such iterators. Let's call them rows. What the algorithm does is this:
- push row0 to the iterator queue
- yield (row0.next, y0)
- push row1 to the iterator queue
- yield (row0.next, y0) (first iterator from iterator queue)
- yield (row1.next, y1) (second (last) iterator from iterator queue)
- push row2 to the iterator queue
- yield (row0.next, y0) (that is, (x2,y0))
- yield (row1.next, y1) (that is, (x1,y1))
- yield (row2.next, y2) (that is, (x0,y2))
and so on: every time we reach the end of the queue, we push the next row iterator into the queue, reset the vertical iterator, and start all over.
The problem arises when one of the iterators is out of elements.
We have two possible cases.
Case 1. The vertical iterator halts. In this case we stop pushing new iterators into the queue, so that the size of the queue is the size of the vertical component.
Case 2. the horizontal iterator halts. The vertical one may be infinite or not, we have to shift it. E.g. if we build
{'A', 'B','C'} x N, we will be producing
('A',0), ('B',0), ('A',1), ('C',0), ('B',1), ('A',2), ('C',1), ('B',2), ('A',3).... Note that after
('C',1) row0 is out of elements, and this row should be dropped from the queue. At the same time the beginning element of the vertical iterator should be shifted, so that the next loop will be not
0,1,2, but
1,2,3. In such a way we go all along the vertical iterator.
Here's the code:
def kantorIterator[X, Y](xs: Iterable[X], ys: Iterable[Y]): Iterator[(X, Y)] =
new Iterator[(X, Y)] {
var iterators: Queue[Iterator[Y]] = Queue()
var xi = xs.iterator
var yi: Iterator[Iterator[Y]] = Iterator.empty
var shift = 0
def next = {
if (!yi.hasNext) {
if (xi.hasNext) {
iterators enqueue ys.iterator
}
yi = iterators.iterator
xi = xs.iterator.drop(shift)
}
val yii = yi.next
val y = yii.next
val res = (xi.next, y)
if (!iterators.isEmpty && yii.isEmpty) {
iterators.dequeue
shift += 1
}
res
}
def hasNext = !xs.isEmpty && !ys.isEmpty &&
(xi.hasNext || (!iterators.isEmpty && iterators(0).hasNext))
}
hasNext covers all the cases of empty components.
I probably have to mention that you won't be always able to iterate over all the subsets of a countable set. If the set is finite, it's okay, its powerset is finite; but if it is not,
here you can find Kantor's proof that the powerset of an infinite countable set is not countable.
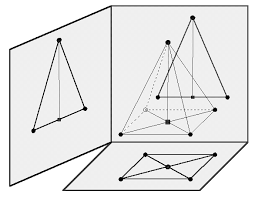the pyramid here is neither a square nor a triangle. But when projected, it can be percieved as one. If we say "he's a soldier", it does not mean that's all the person is; what we mean is just a projection.